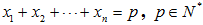
Considere-se a equação x₁ + x₂ + x₃ + x₄ = 7 (I). Suas soluções são listas de números inteiros não negativos da forma (x₁, x₂, x₃, x₄), que, substituídos na equação, tornam a igualdade verdadeira. Algumas soluções dessa são: (0, 0, 3, 4), (1, 0, 0, 6), (2, 0, 5, 0), (1, 2, 1, 3), (0, 0, 0, 7).

Nessa equação x_i   0 para todo i do conjunto {1, 2, 3, 4}. Substituindo cada incógnita x_i por y_i – 1, temos y_i  1 , isto é, y_i é um número inteiro positivo, tendo a equação resultante a forma abaixo (II):

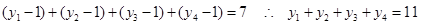
O número de soluções inteiras e não negativas da equação ( I ) de incógnitas x_i é igual ao número de soluções inteiras e positivas da equação ( II ) de incógnitas y_i. Conforme o estudo anterior esse número é igual a:

Considere agora quatro gavetas distintas – A, B, C e D – para guardar sete objetos iguais a . Vamos calcular de quantos modos diferentes é possível arrumar esses objetos nas quatro gavetas, considerando que cada uma pode ficar sem objetos ou com no máximo até os sete objetos . Observe o exemplo a seguir.

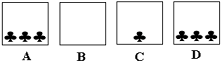
Pode-se então imaginar um objeto colocado em cada uma das três gavetas e distribuir mais 7. Isso corresponde a arrumar 4 + 7 = 11 objetos em quatro gavetas distintas de modo que cada gaveta contenha pelo menos um objeto. Logo, recai-se no problema exposto na parte 1 deste artigo, que é arrumar objetos iguais em gavetas, considerando que cada gaveta deve ficar com pelo menos um objeto. Tem-se assim o número de arrumações igual a .

Pode-se considerar também que as gavetas A, B, C e D vão guardar, respectivamente, x₁, x₂, x₃ e x₄ objetos, sendo  x_i   0. Neste caso, o número de modos de guardar os sete objetos corresponde ao número de soluções inteiras não negativas da seguinte equação, que foi resolvida inicialmente:

x₁ + x₂ + x₃ + x₄ = 7

Generalizando, o número de soluções inteiras e não negativas de x₁ + x₂ + x₃ + ... + x_n = p é igual ao número de soluções inteiras e positivas de (y₁–1) + (y₂–1) + (y₃–1) + ... + (y_n–1) = p ou de y₁ + y₂ + y₃ + ... + y_n = p + n. Esse resultado corresponde ao número de modos de guardar p objetos iguais em n gavetas (quando em cada uma delas pode conter até todos os objetos) e corresponde a:

Pela propriedade das combinações complementares, tem-se:

Combinações completas ou com repetição de elementos

Considere os grupos de p objetos, distintos ou não, selecionados de um conjunto de n objetos, que poderão ser escolhidos em um evento, sem que se leve em conta a ordem da escolha. Cada um desses grupos, que pode ter no máximo até p objetos iguais, é uma combinação completa de classe p dos n elementos disponíveis.

As tabelas a seguir mostram combinações dos elementos distintos do conjunto {a, b, c, d}.

Combinações simples de quatro elementos tomados 2 a 2		Combinações completas de quatro elementos tomados 2 a 2
ab ac ad  bc bd  cd		aa ab ac ad  bb bc bd  cc cd  dd
Combinações simples de quatro elementos tomados 3 a 3		Combinações completas de quatro elementos tomados 3 a 3
abc abd acd  bcd		aaa aab aac aad abb acc add abc abd acd  bbb bbc bbd bcc bdd bcd  ccc ccd  ddd ddc

As combinações são grupos não ordenados e só existe uma combinação simples desses quatro elementos tomados 4 a 4 que é (abcd), entretanto não é possível formar combinações simples dos mesmos elementos com grupos de cinco elementos. Existem combinações completas desses quatro elementos tomados 5 a 5, porque nestas é permitido repetir elementos. Alguns exemplos dessas combinações são aaaaa, abbbb, bbccc, abcda.

Se uma pessoa deseja comprar três refrigerantes em uma loja que vende cinco sabores diferentes – A, B, C, D ou E –, tem-se uma situação em que p = 3 e n = 5. Duas compras são diferentes apenas pela quantidade ou pela diferença dos sabores comprados; assim, AAA, BBE, ABC ou CDD são alguns exemplos de compras diferentes. Para calcular o número total de compras distintas que podem ser feitas, suponha que x₁, x₂, x₃, x₄ e x₅ sejam os números de refrigerantes, respectivamente, dos tipos A, B, C, D e E, que serão comprados. Então:

x₁ + x₂ + x₃ + x₄ + x₅ = 3

Observe a tabela com algumas compras que podem ser realizadas:

Compras	x1	x2	x3	x4	x5
AAA	3	0	0	0	0
BBE	0	2	0	0	1
ABC	1	1	1	0	0
CDD	0	0	1	2	0

Como x_i   0, cada compra corresponde a uma solução inteira e não negativa dessa equação. De acordo com o estudo anterior, o número total de possibilidades de efetuar essa compra corresponde a:

Assim, o número de combinações completas ou com repetição de n objetos distintos tomados p a p, representado por , é igual ao número de soluções inteiras não negativas da equação x₁ + x₂ ... x_n = p . Para esta equação,

x₁ = número de elementos do 1º objeto,
x₂ = número de elementos do 2º objeto,

(...)
x_n = número de elementos do enésimo objeto.

Logo, , isto é, o número de combinações com repetição de n elementos tomados p a p corresponde ao número de combinações simples de n + p – 1 elementos tomados p a p.

Gostaríamos de ressaltar que, de uma forma simplificada, a análise combinatória consiste no estudo dos modos de contar agrupamentos de elementos sujeitos a regras específicas e, também, no estudo das propriedades desses agrupamentos. Em problemas simples do cotidiano, usamos argumentos dessa área da matemática discreta, como gostaria de ilustrar. Vinte alunos da minha turma vão votar nos quatro candidatos à presidência do Brasil. Naturalmente, cada pessoa só pode votar em um candidato. Considerando apenas o número de votos dados a cada um dos candidatos, quantas possíveis distribuições de votos existem?

Se x₁, x₂, x₃ e x₄ são, respectivamente, os números de votos dos candidatos A, B, C e D, então x₁ + x₂ + x₃ + x₄= 20, e o número de soluções inteiras, não negativas, pode ser descrito pela fórmula a seguir:

Esse valor corresponde ao número total de distribuições de votos que podem ocorrer.

Todos os ramos da matemática têm os seus aspectos combinatórios. Há na aritmética, na topologia, na lógica, na geometria, entre outros, a necessidade de se recorrer à combinatória. Em particular, a análise combinatória é essencial na teoria das probabilidades.

Finalizo estes dois artigos que abordam a importância dos métodos de contagem, lembrando que esse tópico da matemática discreta é tão importante que Gottfried Wilhelm Leibniz (1646-1716), que contribuiu muito com as teorias das probabilidades e da análise combinatória, na sua obra Dissertação sobre a arte da combinatória, concluiu que todo raciocínio dedutivo, tanto na matemática quanto na lógica pura, lida com combinações de símbolos em cadeia, de acordo com as regras de um sistema, que decide se a cadeia é uma proposição válida ou não.

Referências:

- A matemática no ensino médio, de Elon Lages Lima e outros, publicado pela Editora SBM.

- Análise combinatória e probabilidade, de A. C. Morgado, publicado pela Editora SBM.

- Prelúdio à análise combinatória, de Arago de C. Bachx, publicado pela Companhia Editora Nacional.