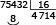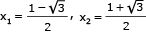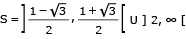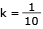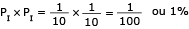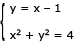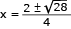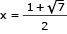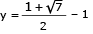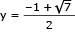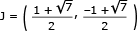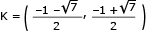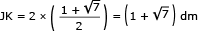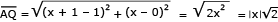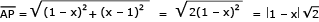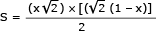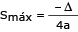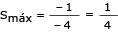Ano 8, n. 24, ano 2015

Técnicos do órgão de trânsito recomendaram velocidade máxima de 80 km/h no trecho de uma rodovia onde ocorrem muitos acidentes. Para saber se os motoristas estavam cumprindo as recomendações, foi instalado um radar móvel no local. O aparelho registrou os seguintes resultados percentuais relativos às velocidades dos veículos ao longo de trinta dias, conforme o gráfico abaixo:
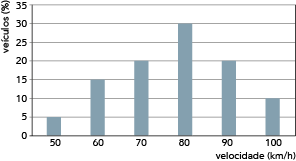
Determine a média de velocidade, em km/h, dos veículos que trafegaram no local nesse período.
Objetivo: Calcular média aritmética de valores apresentados em gráfico.
Item do programa: Medidas de tendência central
Subitem do programa: Médias aritmética, geométrica, harmônica
Comentário da questão:
A média de velocidade dos veículos corresponde à razão entre a soma de todas as velocidades e a quantidade total de veículos, que é dada em porcentagem. A soma das velocidades dos veículos pode ser obtida pela soma de cada velocidade indicada no gráfico multiplicada pela quantidade de veículos. Trata-se da frequência de cada velocidade:
5 × 50 + 15 × 60 + 20 × 70 + 30 × 80 + 20 × 90 + 10 × 100 = 7750
O número total de veículos, em porcentagem, equivale a:
5 + 15 + 20 + 30 + 20 + 10 = 100
Logo:
Média = 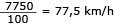
Ano 8, n. 24, ano 2015

Na região conhecida como Triângulo das Bermudas, localizada no oceano Atlântico, é possível formar um triângulo com um vértice sobre a cidade porto-riquenha de San Juan, outro sobre a cidade estadunidense de Miami e o terceiro sobre as ilhas Bermudas.
A figura abaixo mostra um sistema de coordenadas cartesianas ortogonais, com os vértices do triângulo devidamente representados. A escala utilizada é 1:17.000.000, e cada unidade nos eixos cartesianos equivale ao comprimento de 1 cm.
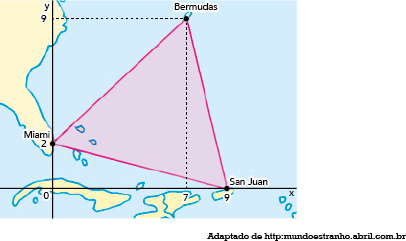
Calcule, em km2, a área do Triângulo das Bermudas, conforme a representação plana da figura.
Objetivo: Calcular área de um triângulo representado em um plano cartesiano.
Item do programa: Polígonos e círculos
Subitem do programa: Áreas
Comentário da questão:
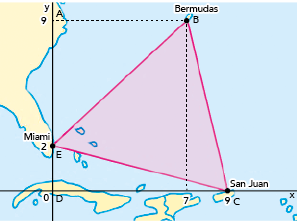
O triângulo em análise possui vértices E(0, 2), B(7, 9) e C(9, 0).
Observe na imagem o trapézio ABCD e os triângulos retângulos ABE e EDC. Note que a área do triângulo BEC é dada por: Área do trapézioABCD – Área do triânguloABE – Área do triânguloEDC.

Como a escala é 1:17.000.000, a razão entre as áreas é a razão linear ao quadrado, ou seja, (1/17.000.000)2. Desse modo, constrói-se a seguinte proporção:
Assim, a área do triângulo das Bermudas é:
Para solucionar esta questão, pode-se considerar também que a área do triângulo corresponde à metade do determinante de uma matriz obtida a partir dos vértices, sendo a terceira coluna completada por 1:
Ano 8, n. 24, ano 2015

Com o objetivo de melhorar o tráfego de veículos, a prefeitura de uma grande cidade propôs a construção de quatro terminais de ônibus. Para estabelecer conexão entre os terminais, foram estipuladas as seguintes quantidades de linhas de ônibus:
• do terminal A para o B, 4 linhas distintas;
• do terminal B para o C, 3 linhas distintas;
• do terminal A para o D, 5 linhas distintas;
• do terminal D para o C, 2 linhas distintas.
Não há linhas diretas entre os terminais A e C.
Supondo que um passageiro utilize exatamente duas linhas de ônibus para ir do terminal A para o terminal C, calcule a quantidade possível de trajetos distintos que ele poderá fazer.
Objetivo: Calcular a quantidade de possibilidades distintas de um evento.
Item do programa: Contagem
Subitem do programa: -
Comentário da questão:
Para fazer o trajeto do terminal A até o terminal C, pode–se passar tanto pelo terminal B quanto pelo D.
Passando por B, devem-se considerar as seguintes quantidades de linhas de ônibus:
A para B = 4
B para C = 3
Total de trajetos possíveis = 4 × 3 = 12
Passando por D, devem-se considerar as seguintes quantidades de linhas de ônibus:
A para D = 5
D para C = 2
Total de trajetos possíveis = 5 × 2 = 10
Dessa forma, o total de trajetos distintos de A para C corresponde a 12 + 10 = 22.
Ano 8, n. 24, ano 2015

Em 1965, o engenheiro Gordon Moore divulgou em um artigo que, a cada ano, a indústria de eletrônicos conseguiria construir um processador com o dobro de transistores existentes no mesmo processador no ano anterior. Em 1975, ele atualizou o artigo, afirmando que, de fato, a quantidade de transistores dobraria a cada dois anos. Essa última formulação descreve uma progressão que ficou conhecida como Lei de Moore e que permite afirmar que um processador que possuía 144 × 102 transistores em 1975 evoluiu para um processador com 288 × 102 transistores em 1977.
Admitindo um processador com 731 × 106 transistores em 2009, calcule a quantidade de transistores que a evolução desse processador possuirá em 2019, segundo a Lei de Moore.
Objetivo: Calcular um termo de uma sequência geométrica.
Item do programa: Progressões
Subitem do programa: Geométricas
Comentário da questão:
O problema aborda uma sequência geométrica, em que o primeiro termo equivale ao ano de 2009 e o sexto ao ano de 2019. Tem-se, assim, uma sequência com seis termos e razão 2. Observe a equação geral da PG:
an = a1 × qn – 1
sendo
an = um termo qualquer de ordem n
a1 = primeiro termo
q = razão da progressão geométrica
Logo:
1º termo (2009) = 731 × 106
6º termo (2019) = a1 × 25 = 731 × 106 × 32 = 23392 × 106
Logo, em 2019, o processador possuirá 23.392.000.000 transistores.
Ano 8, n. 24, ano 2015

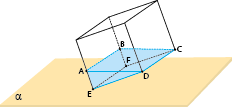
Um prisma triangular reto ABCDEF foi dividido em duas partes por um plano α, de acordo com a imagem abaixo. Os ângulos 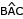 e
e  das bases do prisma são retos, e o plano a contém os pontos A, B e G, sendo que G pertence à aresta CF e dista 4 cm de C.
das bases do prisma são retos, e o plano a contém os pontos A, B e G, sendo que G pertence à aresta CF e dista 4 cm de C.
Calcule o volume, em cm3, do maior sólido definido pela separação estabelecida no prisma pelo plano α.
Objetivo: Calcular o volume de um poliedro.
Item do programa: Sólidos com arestas
Subitem do programa: Poliedros
Subitem do programa: Prismas
Subitem do programa: Pirâmides
Subitem do programa: Volumes
Comentário da questão:
A partir da secção observada na imagem, pode-se reconhecer que o maior sólido é o poliedro de vértices FEDGBA. O volume desse sólido corresponde ao volume do prisma ABCDEF subtraído do volume da pirâmide ABCG:
VFEDGBA = VABCDEF - VABCG
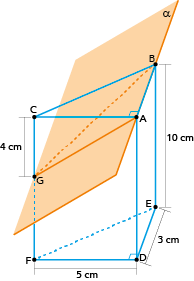
VABCDEF = VPRISMA = AB × h
AB = área do triângulo retângulo com catetos a e b
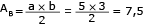
h = 10 cm
Logo:
VABCDEF = 7,5 × 10 = 75 cm3
VABCG = volume de uma pirâmide triangular de base AB e altura CG = h’
Vpirâmide = 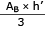
h’ = 4 cm
Logo:
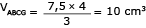
Assim:
VFEDGBA = 75 – 10 = 65 cm3
Ano 8, n. 24, ano 2015

Considere uma matriz A com 3 linhas e 1 coluna, na qual foram escritos os valores 1, 2 e 13, nesta ordem, de cima para baixo.
Considere, também, uma matriz B com 1 linha e 3 colunas, na qual foram escritos os valores 1, 2 e 13, nesta ordem, da esquerda para a direita.
Calcule o determinante da matriz obtida pelo produto de A × B.
Objetivo: Calcular o determinante de uma matriz.
Item do programa: Matrizes
Subitem do programa: Operações
Subitem do programa: Determinantes de 2ª e de 3ª ordens
Comentário da questão:
Considere a matriz coluna A e a matriz linha B:
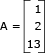
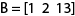
Observe o produto A × B:
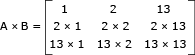
De acordo com a Regra de Sarrus, as duas primeiras colunas são repetidas e aplica-se o procedimento abaixo:
det (A x B) = 

Note-se que, por meio dessa regra, os valores obtidos pelo produto dos elementos das diagonais principais são somados, assim como os das diagonais secundárias. Em seguida, o primeiro total é subtraído do segundo:
4 x 169 + 2 x 26 x 13 + 13 x 2 x 26 – (4 x 169 + 26 x 26 + 4 x 169) = 0
Como as matrizes possuem os mesmos elementos, respectivamente na coluna e na linha, o determinante pode ser obtido sem cálculos. Em consequência disso, a matriz do produto A x B possui colunas, ou linhas, múltiplas entre si. Sempre que as matrizes apresentam essas características, o determinante é nulo.
Ano 8, n. 24, ano 2015

O resultado de um estudo para combater o desperdício de água, em certo município, propôs que as companhias de abastecimento pagassem uma taxa à agência reguladora sobre as perdas por vazamento nos seus sistemas de distribuição. No gráfico, mostra-se o valor a ser pago por uma companhia em função da perda por habitante.
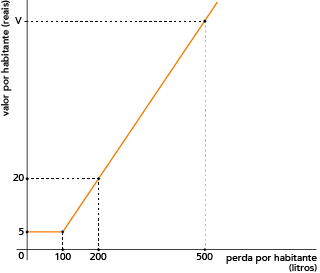
Calcule o valor V, em reais, representado no gráfico, quando a perda for igual a 500 litros por habitante.
Objetivo: Calcular o valor de uma ordenada para um valor conhecido de uma abscissa em um gráfico de uma reta no plano cartesiano.
Item do programa: Geometria analítica no R2
Subitem do programa: Reta
Comentário da questão:
A equação da reta pode ser dada por:
y – yo = m (x – xo)
Seja m o coeficiente angular da reta dado por:
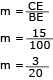
Seja B um ponto da reta:
B (100, 5)
Assim a reta BD é dada por:
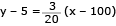
Como ED pertence à reta BD, tem-se:
D (500, v)
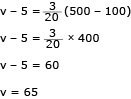
Também é possível solucionar esse problema por semelhança de triângulos.
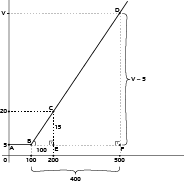
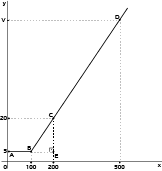
Na representação gráfica, o segmento BD, por ser linear, possui taxa de variação constante para o intervalo de 100 a 500. Desse modo, é possível construir dois triângulos semelhantes conforme as figuras abaixo, sendo BCE semelhante a BDF. Logo, por semelhança de triângulos, têm-se:
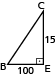
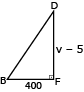
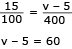
V= 60 + 5 = 65
Ano 8, n. 24, ano 2015

Em uma urna, foram colocadas trinta bolas, numeradas de 1 a 30. Uma dessas bolas foi sorteada aleatoriamente. Em relação a essa experiência, considerem-se os dois eventos abaixo.
Evento A: {a bola sorteada tem número menor ou igual a 20}.
Evento B: {a bola sorteada tem número maior do que k}.
Sabendo que k < 20, k 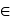 IN e P(A
IN e P(A  B) =
B) = 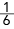 , determine o valor de k.
, determine o valor de k.
Objetivo: Calcular o valor de uma incógnita com base nas condições dadas para dois eventos.
Item do programa: Probabilidades e binômio de Newton
Subitem do programa: Probabilidade condicional
Subitem do programa: União e interseção de eventos
Comentário da questão:
O problema apresenta dois eventos, A e B, com elementos comuns. Assim, é possível aplicar a probabilidade total, somando as probabilidades de cada um dos eventos e subtraindo a probabilidade referente aos elementos comuns.
P(A) + P(B) – P(A B) = 1
B) = 1

Os elementos de B iniciam em k + 1 e terminam em 30:
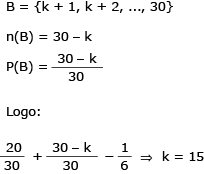
Observe outra resolução possível.
Sendo P(A  B)=
B)= 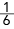 =
= 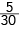 , tem-se n(A
, tem-se n(A  B) = 5. O evento A = {1, 2, ..., 20} e o evento B = {k + 1, k + 2, ..., 30} possuem cinco elementos em comum, podendo-se inferir que A
B) = 5. O evento A = {1, 2, ..., 20} e o evento B = {k + 1, k + 2, ..., 30} possuem cinco elementos em comum, podendo-se inferir que A  B = {16, 17, 18, 19, 20}.
B = {16, 17, 18, 19, 20}.
Logo:
k + 1 = 16
k = 15
Ano 8, n. 24, ano 2015

Em um triângulo equilátero de perímetro igual a 6 cm, inscreve-se um retângulo de modo que um de seus lados fique sobre um dos lados do triângulo. Observe a figura:

Admitindo que o retângulo possui a maior área possível, determine, em centímetros, as medidas x e y de seus lados.
Objetivo: Calcular as medidas de um retângulo de área máxima inscrito em um triângulo equilátero.
Item do programa: Função quadrática
Subitem do programa: Máximo
Comentário da questão:
Observe a figura:

O retângulo de lados x e y está inscrito em um triângulo equilátero de lado igual a 2 cm. Seu lado x está sobre um dos lados do triângulo. Aplicando-se o teorema de Pitágoras ao triângulo retângulo ADC, pode-se determinar o valor de AD, que corresponde à altura h do triângulo ABC. Considerando as propriedades das figuras envolvidas e, portanto, a semelhança dos triângulos ABD e EBF, constrói-se a seguinte equação:
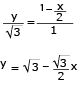
Desse modo, tem-se a área do retângulo, dada pelo produto x.y:
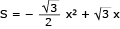
A área máxima do retângulo será dada pelo valor máximo da equação:
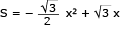
Deve-se lembrar que S = ax2 + bx + c, logo:
Assim:
x = 1
Ano 8, n. 24, ano 2015

Na figura abaixo, observa-se o retângulo ABCD, que contém o triângulo retângulo DEF, no qual DF = 1.
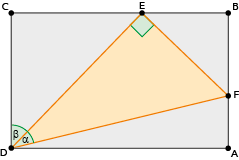
Considerando os ângulos  = α e
= α e  = β, determine o comprimento do lado DA em função de α e β.
= β, determine o comprimento do lado DA em função de α e β.
Objetivo: Calcular o comprimento de um lado de um retângulo em função de ângulos dados.
Item do programa: Polígonos e círculos
Subitem do programa: Relações métricas e angulares
Comentário da questão:
De acordo com a figura, CD é paralelo a BF. Como DF corta os segmentos paralelos, o ângulo que DF forma com CD é igual ao ângulo que DF forma com BA. Desse modo, pode-se escrever:
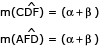
Aplicando o seno deste ângulo no triângulo ADF, tem-se:
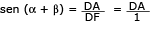
Então:

Pode-se solucionar o problema também pelo cosseno. Observe:
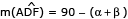
Aplicando o cosseno deste ângulo no triângulo ADF, tem-se:
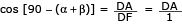
Então:
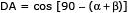
Ano 7, n. 20, ano 2014
O cartão pré-pago de um usuário do metrô tem R$8,90 de crédito. Para uma viagem, foi debitado desse cartão o valor de R$ 3,25, correspondente a uma passagem. Em seguida, o usuário creditou mais R$ 20,00 nesse mesmo cartão.
Admitindo que o preço da passagem continue o mesmo, e que não será realizado mais crédito algum, determine o número máximo de passagens que ainda podem ser debitadas desse cartão.
Objetivo: Calcular uma divisão.
Item do programa: Números reais
Subitem do programa: Operações
Comentário da questão:
Após o débito, restou no cartão o saldo de 8,90 – 3,25 = 5,65; com o crédito, o saldo passou a 5,65 + 20,00 = 25,65. O número de passagens que ainda pode ser debitado é, no máximo, o quociente da divisão de 25,65 por 3,25, que corresponde a 7.
Ano 7, n. 20, ano 2014
Leia a tirinha:

Suponha que existam exatamente 700 milhões de analfabetos no mundo e que esse número seja reduzido, a uma taxa constante, em 10% ao ano, totalizando n milhões daqui a três anos.
Calcule o valor de n.
Objetivo: Calcular uma porcentagem.
Item do programa: Números reais
Subitem do programa: Proporções e porcentagens
Comentário da questão:
Considerando a redução a uma taxa constante de 10% ao ano, o total de analfabetos ao longo de três anos corresponde a:
• 700 × 106 × (0,9) = 630.000.000 ao final do 1º ano;
• 700 × 106 × (0,9)2, ou 630.000.000 × 0,9 = 567.000.000, ao final do 2º ano;
• 700 × 106 × (0,9)3, ou 567.000.000 × 0,9 = 510.300.000, ao final do 3º ano.
Portanto, em três anos, haverá 700 × 106 × (0,9)3 = 510,3 milhões de adultos analfabetos.
Ano 7, n. 20, ano 2014
Uma ferramenta utilizada na construção de uma rampa é composta pela seguinte estrutura:
• duas varas de madeira, correspondentes aos segmentos AE e AD, que possuem comprimentos diferentes e formam o ângulo DÂE igual a 45º;
• uma travessa, correspondente ao segmento BC, que une as duas varas e possui uma marca em seu ponto médio M;
• um fio fixado no vértice A e amarrado a uma pedra P na outra extremidade;
• nesse conjunto, os segmentos AB e AC são congruentes.
Observe o esquema que representa essa estrutura:
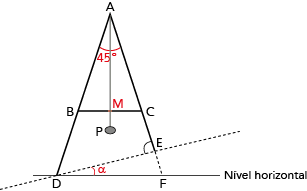
Quando o fio passa pelo ponto M, a travessa BC fica na posição
horizontal. Com isso, obtém-se, na reta que liga os pontos D e E, a
inclinação  desejada.
desejada.
Calcule  , supondo que o ângulo AÊD mede 85º.
, supondo que o ângulo AÊD mede 85º.
Objetivo: Calcular a medida de um âmgulo.
Item do programa: Polígonos e círculos
Subitem do programa: Relações métricas e angulares
Comentário da questão:
Observe a figura:
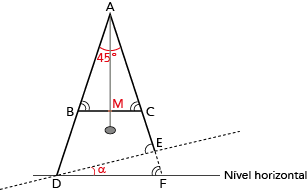
Como 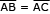 , o triângulo ABC é isósceles. Logo,
, o triângulo ABC é isósceles. Logo, 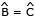 .
.
Assim:
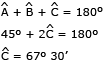
A travessa BC é paralela à reta horizontal DF, então 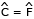 .
.
Considerando o triângulo DEF, tem-se:
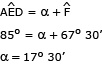
Ano 7, n. 20, ano 2014
Um cubo de aresta EF medindo 8 dm contém água e está apoiado sobre um plano 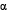 de modo que apenas a aresta EF esteja contida nesse plano. A figura abaixo representa o cubo com a água.
de modo que apenas a aresta EF esteja contida nesse plano. A figura abaixo representa o cubo com a água.
Considere que a superfície livre do líquido no interior do cubo seja um retângulo ABCD com área igual a 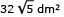 .
.
Determine o volume total, em dm3, de água contida nesse cubo.
Objetivo: Calcular o volume de um prisma.
Item do programa: Sólidos com arestas
Subitem do programa: Prismas
Subitem do programa: Volumes
Comentário da questão:
Em relação ao cubo, sabe-se que:
• área do retângulo ABCD = 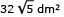
• 
Portanto:

Em relação ao triângulo retângulo AED, tem-se que:

O volume de água no cubo é igual ao volume do prisma de base triangular AED e altura  , então:
, então:

Ano 7, n. 20, ano 2014
Em uma escola circulam dois jornais: Correio do Grêmio e O Estudante. Em relação à leitura desses jornais, por parte dos 840 alunos da escola, sabe-se que:
• 10% não leem esses jornais;
• 520 leem o jornal O Estudante;
• 440 leem o jornal Correio do Grêmio.
Calcule o número total de alunos do colégio que leem os dois jornais.
Objetivo: Calcular o número de elementos de um conjunto.
Item do programa: Noções de conjuntos
Subitem do programa: Operações
Subitem do programa: Representações
Comentário da questão:
Como há 840 alunos na escola e 10% deles não leem os jornais, então 840 – 84 = 756 alunos leem pelo menos um dos jornais. Se 520 alunos leem o jornal O Estudante e 440 leem o Correio do Grêmio, então (520 + 440) – 756 = 204 alunos leem os dois jornais.
De outro modo:
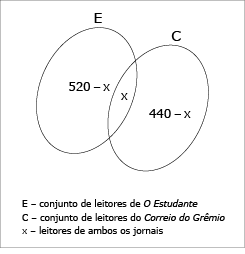
520 – x + x + 440 – x = 756
– x = 756 – 960
– x = – 204
x = 204
Ano 7, n. 20, ano 2014
Ao digitar corretamente a expressão log10(–2) em uma calculadora, o retorno obtido no visor corresponde a uma mensagem de erro, uma vez que esse logaritmo não é um número real.
Determine todos os valores reais de x para que o valor da expressão log0,1(log10(log0,1(x))) seja um número real.
Objetivo: Calcular um logaritmo.
Item do programa: Funções logarítmicas e exponenciais
Subitem do programa: Inequações
Comentário da questão:
log0,1 (log10(log0,1(x))) é um número real nas seguintes condições:
(I)
x > 0
(II)
log0,1(x) > 0
log0,1(x) > log0,1(1)
x < 1
(III)
log10(log0,1(x)) > 0
log0,1(x) > 1
log0,1(x) > log0,1(0,1)
x < 0,1
Com base em (I), (II) e (III), para que o valor da expressão seja um número real, 0 < x < 0,1.
Ano 7, n. 20, ano 2014
Um tubo cilíndrico cuja base tem centro F e raio r rola sem deslizar sobre um obstáculo com a forma de um prisma triangular regular. As vistas das bases do cilindro e do prisma são mostradas em três etapas desse movimento, I, II e III, nas figuras a seguir.

Admita que:
• as medidas do diâmetro do círculo de centro F e da altura do triângulo ABC são respectivamente
iguais a 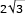 decímetros;
decímetros;
• durante todo o percurso, o círculo e o triângulo sempre se tangenciam.
Determine o comprimento total, em decímetros, do caminho descrito pelo centro F do círculo que representa a base do cilindro.
Objetivo: Calcular o comprimento de um arco de circunferência e de um segmento de reta.
Item do programa: Polígonos e círculos
Subitem do programa: Relações métricas e angulares
Item do programa 2: Sólidos com arestas
Subitem do programa: Prismas
Item do programa 3: Sólidos sem arestas
Subitem do programa: Cilindros
Comentário da questão:
O caminho percorrido pelo centro F corresponde a um conjunto de pontos cuja distância aos lados AC e BC e ao vértice C, do triângulo ABC, é constante e igual ao raio r da base do cilindro. Na figura abaixo, esse caminho está representado por F1F2F3F4.

Conhecendo-se a altura, pode-se calcular o lado l do triângulo equilátero ABC:
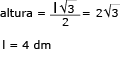
Do mesmo modo, pode-se calcular o raio r da base do cilindro:
diâmetro = 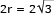
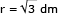
Em relação ao triângulo retângulo AF1T1, tem-se:
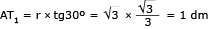
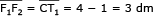
Logo:
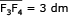
Considere-se agora o arco de circunferência:
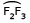
Seu ângulo central corresponde a:
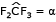
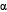 + 90º + 90º + 60º = 360º
+ 90º + 90º + 60º = 360º
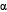 = 120º
= 120º
Assim, a medida desse arco é igual a 1/3 da circunferência:
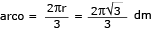
Portanto, o comprimento de F1F2F3F4 equivale a:
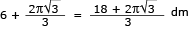
Ano 7, n. 20, ano 2014

Considere a função real f, de variável real x, definida pelo seguinte determinante:
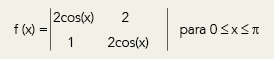
Observe o gráfico da função f.
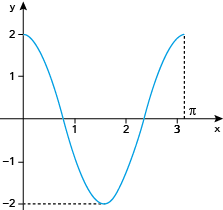
Determine os valores de x para os quais f(x) = 1.
Objetivo: Calcular as raízes de uma equação trigonométrica.
Item do programa: Funções trigonométricas
Subitem do programa: Equações
Item do programa 2: Matrizes
Subitem do programa: Determinantes de 2ª e de 3ª ordens
Comentário da questão:
Resolvendo o determinante, tem-se:
f(x) = 4(cosx)2 – 2 = 1
4(cosx)2 = 3
(cosx)2 = 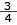
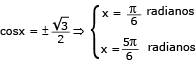
Outra solução possível:
f(x) = 4(cosx)2 – 2
f(x) = 2(2(cosx)2 – 1)
f(x) = 2cos(2x)
Como f(x) = 1, então:
2cos(2x) = 1
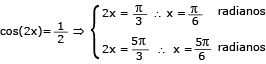
Ano 7, n. 20, ano 2014
Uma ferrovia foi planejada para conter um trecho retilíneo cujos pontos são equidistantes dos centros A e B de dois municípios. Em seu projeto de construção, utilizou-se o plano cartesiano, com coordenadas em quilômetros, em que A = (1, 2) e B = (7, 14). Observe o gráfico:
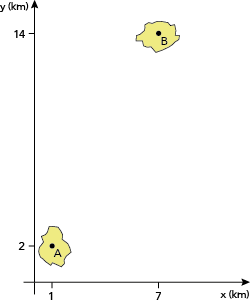
Determine, utilizando esse sistema referencial, a equação da reta suporte desse trecho retilíneo da ferrovia.
Objetivo: Calcular a equação de uma reta.
Item do programa: Geometria analítica no R2
Subitem do programa: Reta
Comentário da questão:
O ponto médio M do segmento AB é obtido por:
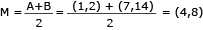
O coeficiente angular m da reta r que passa pelos pontos A(1,2) e B(7,14) é igual a:
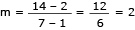
O coeficiente angular m1 da reta r1 perpendicular à reta r é igual a:
mm1 = –1
2m1 = –1
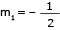
A equação da reta r1 que passa pelo ponto médio M é:
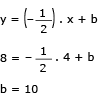
Logo:
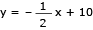
Outra solução é apresentada a seguir.
Se P(x,y) é um ponto equidistante de A(1,2) e B(7,14), então:
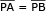
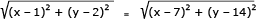
x2 – 2x + 1 + y2 – 4y + 4 = x2 – 14x + 49 + y2 – 28y + 196
12x + 24y = 240
x + 2y = 20
Ano 7, n. 20, ano 2014

Cada uma das 28 peças do jogo de dominó convencional, ilustradas abaixo, contêm dois números, de zero a seis, indicados por pequenos círculos ou, no caso do zero, por sua ausência.
Admita um novo tipo de dominó, semelhante ao convencional, no qual os dois números de cada peça variem de zero a dez. Observe o desenho de uma dessas peças:

Considere que uma peça seja retirada ao acaso do novo dominó. Calcule a probabilidade de essa peça apresentar um número seis ou um número nove.
Objetivo: Calcular uma probabilidade.
Item do programa: Contagem
Subitem do programa: Combinações
Comentário da questão:
O número total de peças do novo dominó é igual ao de combinações com repetição CR de onze números {0, 1, 2, ..., 10} tomados dois a dois, ou seja:
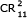
Isso equivale ao número de combinações simples C de dez elementos tomados dois a dois, isto é:
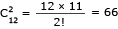
Existem onze peças com seis círculos em uma de suas metades e onze com nove círculos, sendo uma peça comum aos dois conjuntos. Assim, existem 11 + 11 – 1 = 21 peças com seis ou com nove círculos.
Então, a probabilidade de retirar uma peça, ao acaso, e ela ter seis ou nove círculos corresponde a:
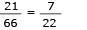
Outro modo de contar o número de peças é observar a disposição dos pares ordenados associados às peças do novo dominó. Observe uma representação parcial dessa disposição:

Somando-se o número de peças de todas as colunas, tem-se:
11 + 10 + 9 + 8 +7 + 6 + 5 +4 +3 + 2 + 1 = 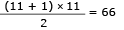
Portanto, a possibilidade de retirar uma peça ao acaso, nas condições indicadas, é:
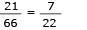
Ano 6, n. 18, ano 2013

Considere um participante da campanha que receba 16 g de ouro pelo número inteiro de quilogramas perdidos.
Sabendo que a massa dessa pessoa, ao receber o prêmio, é de 93,0 kg, determine o valor inteiro de sua massa, em quilogramas, no início da campanha.
Objetivo: Calcular o valor de uma expressão.
Item do programa: Conjuntos numéricos
Subitem do programa: Naturais
Comentário da questão:
Considerando a tabela, quando um participante perde de 1 a 5 kg, ganha de 1 a 5 g de ouro; quando perde de 6 a 10 kg, ganha de 12 a 20 g de ouro. Então, um participante que ganhou 16 g perdeu 8 kg de massa. Inicialmente, portanto, ele tinha 93 + 8 = 101 kg.
Ano 6, n. 18, ano 2013
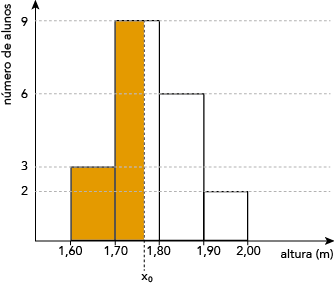
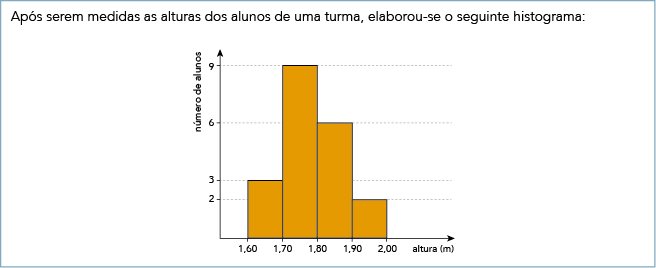
Sabe-se que, em um histograma, se uma reta vertical de equação x = x0 divide ao meio a área do polígono formado pelas barras retangulares, o valor de x0 corresponde à mediana da distribuição dos dados representados.
Calcule a mediana das alturas dos alunos representadas no histograma.
Objetivo: Calcular a mediana de uma distribuição de dados.
Item do programa: Medidas de tendência central
Subitem do programa: Mediana
Item do programa 2: Polígonos e círculos
Subitem do programa: Áreas
Comentário da questão:
A área total do polígono corresponde ao somatório das áreas dos retângulos que constituem o polígono:
A = 0,1

(2 + 3 + 6 + 9) = 2
A metade dessa área, que é igual a 1, está compreendida entre as retas verticais x = 1,60 e x = x0, de modo que 1,70 < x0 < 1,80.
Isso resulta na equação:
0,1  3 + (x0
3 + (x0  1,70)
1,70)  9 = 1
9 = 1
Logo, x0 = 1 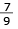 ou x0 = 1,77...
ou x0 = 1,77...
Ano 6, n. 18, ano 2013

Os dados do histograma também podem ser representados em um gráfico de setores. Observe:
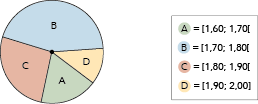
Calcule o maior ângulo central, em graus, desse gráfico de setores.
Objetivo: Calcular uma proporção.
Item do programa: Números reais
Subitem do programa: Razões
Subitem do programa: Proporções e porcentagens
Item do programa 3: Geometria de posição
Subitem do programa: Distâncias e ângulos
Comentário da questão:
O total de 20 alunos da turma corresponde ao ângulo de 360º, então 9 alunos correspondem a x graus. Como o número de alunos é diretamente proporcional ao ângulo central, tem-se a seguinte proporção:
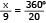
x = 162°
Ano 6, n. 18, ano 2013

Observe o anúncio abaixo, que apresenta descontos promocionais de uma loja.

Admita que essa promoção obedeça à seguinte sequência:
• primeiro desconto de 10% sobre o preço da mercadoria;
• segundo desconto de 10% sobre o valor após o primeiro desconto;
• desconto de R$100,00 sobre o valor após o segundo desconto.
Determine o preço inicial de uma mercadoria cujo valor, após os três descontos, é igual a R$ 710,00.
Objetivo: Calcular uma porcentagem.
Item do programa: Números reais
Subitem do programa: Proporções e porcentagens
Comentário da questão:
O último desconto concedido é de R$ 100,00. Adicionando-se esse valor ao valor final de R$ 710,00, o total é de R$ 810,00. Esse valor, por sua vez, é o resultado de dois descontos sucessivos de 10% no preço inicial da mercadoria. Logo, dividindo-se esse valor por 0,9 duas vezes, sucessivamente, chega-se ao preço inicial:
R$ 810,00 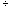 0,9 = R$ 900,00
0,9 = R$ 900,00
R$ 900,00 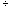 0,9 = R$ 1.000,00
0,9 = R$ 1.000,00
O preço inicial da mercadoria é de R$ 1.000,00.
Ano 6, n. 18, ano 2013

Considere a sequência de matrizes (A1, A2, A3, ...), todas quadradas de ordem 4, respectivamente iguais a:

Sabendo que o elemento aij = 75432 é da matriz An, determine os valores de n, i e j.
Objetivo: Descrever a ordem de uma sequência aritmética.
Item do programa: Matrizes
Subitem do programa: Operações
Item do programa 2: Progressões
Subitem do programa: Aritméticas
Comentário da questão:
Se cada matriz tem 16 elementos, dividindo-se 75432 por 16, encontra-se o valor de n:
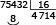
Logo, são 4714 matrizes completas. O número 75432 está na matriz seguinte, ou seja, n = 4715.
A primeira matriz é formada pelos possíveis restos da divisão por 16, e os elementos seguintes têm suas posições determinadas de acordo com os respectivos restos das divisões do elemento por 16.
Como o resto da divisão de 75432 por 16 é 8, a posição desse elemento na matriz é igual à posição do 8 na primeira matriz, ou seja, 75432 = a31. Portanto, i = 3 e j = 1.
Pode-se solucionar esse problema de outra forma. Considere a progressão aritmética formada pelos elementos da primeira linha e da primeira coluna de todas as matrizes:
(0, 16, 32, ... , an, ... ). Então, an = 0 + (n  1) × 16 = 16n
1) × 16 = 16n  16.
16.
16n  16
16 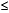 75432
75432
n 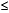 4715,5
4715,5
Logo, o maior valor natural de n é 4715, e a4715 = 75424 ocupa a primeira posição da matriz A4 715. O número 75432 corresponde ao nono elemento dessa matriz, ocupando a terceira linha e a primeira coluna. Portanto, n = 4715, i = 3 e j = 1.
Ano 6, n. 18, ano 2013

O reservatório A perde água a uma taxa constante de 10 litros por hora, enquanto o reservatório B ganha água a uma taxa constante de 12 litros por hora. No gráfico, estão representados, no eixo y, os volumes, em litros, da água contida em cada um dos reservatórios, em função do tempo, em horas, representado no eixo x.
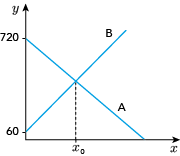
Determine o tempo xo, em horas, indicado no gráfico.
Objetivo: Calcular a abscissa do ponto de intersceção de duas retas.
Item do programa: Função afim
Subitem do programa: Taxa de variação média
Comentário da questão:

As retas representadas no gráfico têm as seguintes equações:
A: y =  10x + 720
10x + 720
B: y = 12x + 60
Para obter a abscissa x0 do ponto de intersecção das duas retas, basta igualar as duas ordenadas:
 10x + 720= 12x + 60
10x + 720= 12x + 60
 22x =
22x =  660
660
x = 30
Logo, x0 = 30 horas.
Ano 6, n. 18, ano 2013
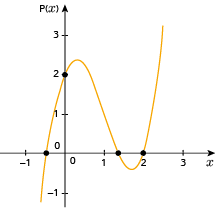
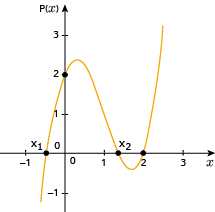
Observe o gráfico da função polinomial de
em
definida por P(
x) = 2
x3 - 6
x2 + 3
x + 2.
Determine o conjunto solução da inequação P(x) > 0.
Objetivo: Calcular o conjunto-solução de uma inequação.
Item do programa: Função polinomial com grau maior do que dois
Subitem do programa: Inequações
Comentário da questão:
Como se observa, o gráfico de P(x) passa pelo ponto (2,0), portanto 2 é uma raiz da equação P(x) = 0.
Logo, P(x) = (x

2).Q(x), ou seja, P(x) é divisível por x

2. Resolvendo a divisão, obtém-se:
Q(x) = 2x
2 
2x

1
Resolvendo a equação Q(x) = 0, determinam-se as outras duas raízes do polinômio P(x).
2x
2 
2x

1 = 0
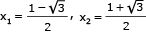
Para resolver a inequação P(x) > 0, determinam-se as abscissas de todos os pontos do gráfico que possuem ordenadas positivas, isto é, que estão acima do eixo x.
Assim, a solução S da inequação consiste na união dos intervalos reais ] x1, x2 [ e ] 2,
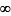
[:
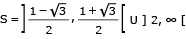
Ano 6, n. 18, ano 2013

Um alvo de dardos é formado por três círculos concêntricos que definem as regiões I, II e III, conforme mostra a ilustração.

Um atirador de dardos sempre acerta alguma região do alvo, sendo suas probabilidades de acertar as regiões I, II e III denominadas, respectivamente, PI, PII e PIII.
Para esse atirador, valem as seguintes relações:
• PII = 3PI
• PIII = 2PII
Calcule a probabilidade de que esse atirador acerte a região I exatamente duas vezes ao fazer dois lançamentos.
Objetivo: Calcular uma probabilidade.
Item do programa: Probabilidades e binômio de Newton
Subitem do programa: União e interseção de eventos
Comentário da questão:
As relações indicadas equivalem a:
PI = k
PII = 3k
PIII = 6k
PI + PII + PIII = 1
10k = 1
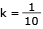
A probabilidade de acertar duas vezes na região I, após dois lançamentos, é:
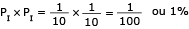
Ano 6, n. 18, ano 2013

Um disco metálico de centro O e diâmetro AB = 4 dm, utilizado na fabricação de determinada peça, é representado pelo seguinte esquema:
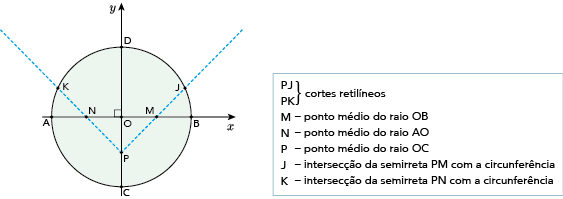
Calcule a distância entre os pontos J e K.
Objetivo: Calcular uma distância entre dois pontos do plano cartesiano.
Item do programa: Geometria analítica no R2
Subitem do programa: Reta
Subitem do programa: Circunferência
Comentário da questão:
A equação da circunferência de centro (0,0) e raio 2 é x2 + y2 = 4. As retas PM e PN têm equações respectivamente iguais a y = x  1 e y =
1 e y =  x
x  1.
1.
Para determinar o ponto J, pertencente ao primeiro quadrante, que é a intersecção da reta PM com a circunferência, resolve-se o sistema a seguir:
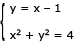
x2 + (x  1)2 = 4
1)2 = 4
2x2  2x
2x  3 = 0
3 = 0
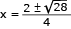
Como o ponto J é do primeiro quadrante, tem-se:
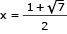
y = x  1
1
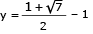
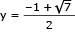
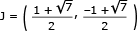
O ponto K está no segundo quadrante, sendo simétrico de J em relação ao eixo y. Assim:
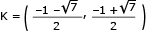
O segmento JK pertence a uma reta horizontal, pois os pontos J e K possuem a mesma ordenada. Logo, a medida de JK é:
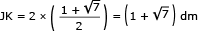
Ano 6, n. 18, ano 2013
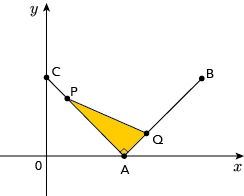
No gráfico acima, estão indicados os pontos A(1,0), B(2,1) e C(0,1), que são fixos, e os pontos P e Q, que se movem simultaneamente. O ponto P se desloca no segmento de reta de C até A, enquanto o ponto Q se desloca no segmento de A até B. Nesses deslocamentos, a cada instante, a abscissa de P é igual à ordenada de Q.
Determine a medida da maior área que o triângulo PAQ pode assumir.
Objetivo: Calcular o máximo de uma função.
Item do programa: Função quadrática
Subitem do programa: Máximo
Item do programa 2: Geometria analítica no R2
Subitem do programa: Reta
Comentário da questão:
Com os pontos A(1,0), B(2,1) e C(0,1), é possível determinar as equações das retas AB e AC:
AB: y = x  1
1
AC: y =  x + 1
x + 1
O ponto P, que está sobre a reta AC, possui abscissa igual à ordenada de Q, que está sobre AB. As coordenadas de P são:
P(x,  x + 1)
x + 1)
Q(x + 1, x)
O triângulo APQ é retângulo em A(1,0), e seus catetos medem AQ e AP.
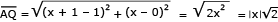
Sendo x > 0, 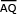 = x
= x 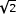 .
.
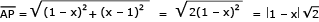
Como 0 < x < 1,  = (1 – x)
= (1 – x) 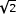 .
.
A área S do triângulo retângulo APQ corresponde a:
S= x

x
2
A área S é uma função polinomial do 2º grau em x. Logo, a área máxima é igual a:
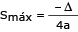
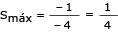


![]()








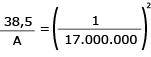

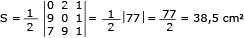




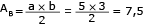
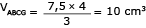

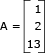
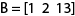
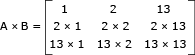





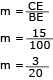
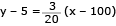
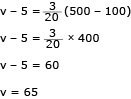



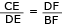
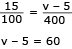


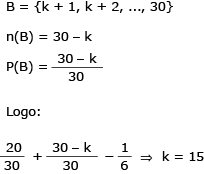



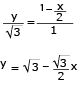
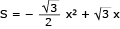
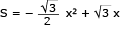
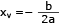
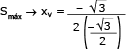
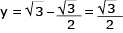


 =
= 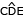 =
= 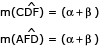
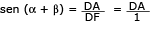

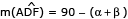
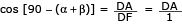
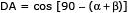






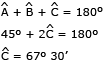
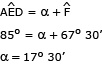











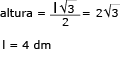
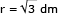
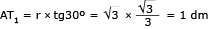
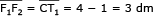
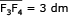
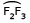
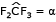
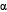 + 90º + 90º + 60º = 360º
+ 90º + 90º + 60º = 360º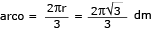
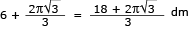

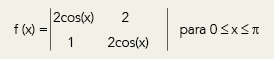

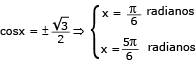
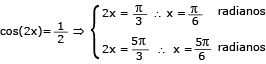


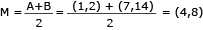
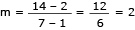
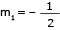
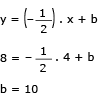
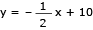
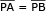
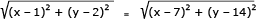



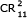
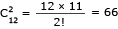
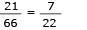




 (2 + 3 + 6 + 9) = 2
(2 + 3 + 6 + 9) = 2

 1,70)
1,70) 

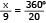


 0,9 = R$ 900,00
0,9 = R$ 900,00